Rasyonel Sayılar Hangileri? Rasyonel Sayıların Özellikleri Ve Büyüklük Küçüklük Bakımından Karşılaştırma

Rasyonel sayılar, öğrencilerin ve sınavlara hazırlanan pek çok kişinin araştırmaları arasında yer alıyor. Matematik dersi altında ele alınan bu konu, rasyonel sayılar nelerdir, rasyonel sayı ne demek gibi sorularla inceleniyor. Bu gruba hangi rakam ve sayıların dahil olduğu merak edilirken, rasyonel sayıların özellikleri de konu kapsamında araştırılıyor. Rasyonel sayılar hangileri? İşte konu anlatımı ile bu konunun ayrıntılı açıklaması!

RASYONEL SAYILAR KONU ANLATIMI

Rasyonel sayılar ya da oranlı sayılar, iki tam sayının birbirine oranı ile ifade edilebilen sayıların oluşturduğu kümedir. Rasyonel sayılar tam sayıların bir genişlemesidir ve {Q} ile gösterilir. Her tam sayı rasyonel sayıdır. Çünkü -3 = -3/1 veya 0 = 0/1 şeklinde yani rasyonel sayı tanımına uygun biçimde yazılabilirler. Sıfırdan büyük olan rasyonel sayılara pozitif rasyonel sayılar, sıfırdan küçük rasyonel sayılar da negatif rasyonel sayılar denir. Pozitif rasyonel sayılar kümesi "Q+"ile gösterilir. Negatif rasyonel sayılar kümesi"Q-"ile gösterilir.

Q = Q- U {0} U Q+

NOT: Her tam sayı rasyonel sayı olarak yazılabilir.

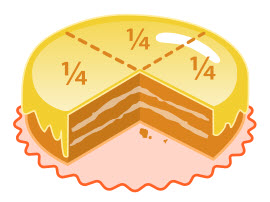
Yukarıdaki şekilde, bir yuvarlak pasta 4 eş parçaya bölünmüş ve bu 4 eş parçalardan her birisi 1/4 olarak görülmektedir. Ancak bir parça alınmış olduğundan kalan eksikdir. Geriye kalan, dört eşit parçaya bölünmüş bütünün üç tane parçası (yani 3'te 4 oranı) veya (kesiri)dir. Bu 3/4 ifadesi şeklinde gösterilir. Burada ifadede kesir çizgisinin üstündeki değere (yani 3'e) pay, kesir çizgisinin altındaki değere (yani 4'e) payda denir. Bu kesir, "üç bölü dört" ya da "dörtte üç" diye okunur.

RASYONEL SAYILAR HANGİLERİ?

• Kesirler
• Doğal sayılar ve tam sayılar
• Ondalık sayılar
• Devirli sayılar
• Bazı karekök sayılar

RASYONEL SAYILARI KARŞILAŞTIRMA (BÜYÜKLÜK, KÜÇÜKLÜK)

Rasyonel sayıları karşılaştırma sırasında pay ve payda eşliğinde eşitleme yapılır. Öte yandan eğer pay ve paydadan biri ya da ikisi negatif ise karşılaştırma buna göre yapılıp sıralanır. Bu durumları sırasıyla ele alacağız.

PAYDALARI EŞİT OLAN RASYONEL SAYILARI KARŞILAŞTIRMA

Paydaları eşit olan pozitif rasyonel sayılarda payı büyük olan daha büyük, payı küçük olan daha küçüktür.
Örnek: 15/20 > 9/20 > 7/20 > 3/20

Paydaları eşit olan negatif rasyonel sayılar pozitifin tam tersidir.Payı büyük olan negatif rasyonel sayılar küçük,payı küçük olan negatif rasyonel sayılar büyüktür.

-3/20 > -7/20 > -9/20 > -15/20

PAYLARI EŞİT OLAN RASYONEL SAYILARI KARŞILAŞTIRMA

Payları eşit olan pozitif rasyonel sayılarda paydası küçük olan daha büyük, paydası büyük olan daha küçüktür.
Örnek: 3/4 > 3/8 > 3/11 > 3/14
Payları eşit olan negatif rasyonel sayılar pozitifin tam tersidir.Paydası büyük olan negatif rasyonel sayılar büyük paydası küçük olan negatif rasyonel sayılar küçüktür.

PAYI VE PAYDALARI FARKLI OLAN RASYONEL SAYILAR

Payı ve paydaları farklı olan rasyonel sayılarda pay paydaya bölünerek sıralama yapılabilir. Bununla birlikte karşılaştırma yapmadan önce paydaların eşitlenmesi veya içler dışar çarpımı yapılması da farklı bir yöntemdir.

Paydaların eşitlenmesi

Her iki rasyonel sayının da birbirlerinin paydalarıyla genişletilmesini gerektirir.

İçler dışlar çarpımı

Birinci rasyonel sayının payının ikincinin paydasına, ikincinin paydasının ise birincinin payıyla çarpılmasıdır:

RASYONEL SAYILARIN EŞİTLİĞİ

İki rasyonel sayının eşitliği, o sayıların pay ve paydalarının rasyonel olmasıyla anlaşılır. a,b,c,d Z kümesinin elemanı olmak üzere a/b ve c/d iki rasyonel sayı ise bu iki sayı ancak a.d = b.c olduğunda eşittir.

Bu koşul, yukarıdaki tanımdan çıkartılabilir. İki rasyonel sayı aynı denklik sınıfındaysa birbirine eşittir, Denklik bağıntısı da zaten a.d = b.c koşulunu içermekteydi.

RASYONEL SAYILARIN CEBİRSEL ÖZELLİKLERİ

Rasyonel sayılar aşağıda gösterildiği gibi birbirlerine eklenir:

Rasyonel sayılar arasındaki çarpma işlemlerinin kuralı aşağıdaki gibidir:

Rasyonel sayılar arasındaki bölme işlemi aşağıda gösterildiği gibidir:

Toplamaya ve çarpmaya göre terslik özellikleri rasyonel sayılar içinde geçerlidir: