Stewart Teoremi Nedir? Stewart Teoremi Formülü, İspatı ve Örnekleri

Stewart Teoremi geometri dersinin bir konusu olarak bilinir. Geometri dersi içerisinde üçgenler konusunda yer almaktadır. Stewart teoremi kullanılıyorsa, üçgenin köşelerinden birinden karşıdaki kenara doğru bir çizgi çizilmektedir. Bu teorem ile ilgili detayları şu sorular ile öğrenebilirsiniz; Stewart Teoremi nedir, Stewart Teoremi nerede kullanılır, Stewart Teoremi ne zaman bulundu, Stewart Teoremi ispatı ve örnekleri nelerdir?

Stewart Teoremi Nedir?

Stewart Teoremi geometride bir üçgenin herhangi bir kenarını kesen doğru ile kesilen kenarın parçaları ve diğer kenarlar arasında kurulan bağlantı olarak bilinir. Bu teoremin adı matematikçi Matthew Stewart'ın onuruna onun adı ile yayınlanmıştır.

Stewart Teoremi Formülü

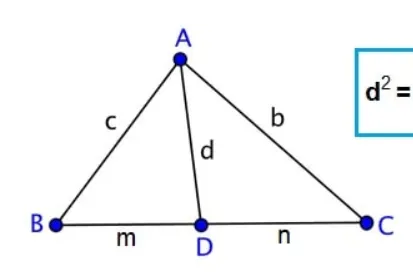
Stewart Teoreminin basit anlatımı aşağıdaki üçgene göre şu şekildedir;

d2 = (c2.n + b2.m) / (m + n) - m.n

Formülü daha iyi hatırlamak istiyorsanız c ile n'nin ve aynı zamanda b ile M'nin çapraz olduğuna dikkat etmelisiniz.

İspatı ve Örnekleri

Bu teoremin ispatı günlük hayatta pek kullanılmaz. Fakat yine de bir şeyin nereden geldiğini bilirsek o şeyi daha çabuk kavrarız ve mantığımıza oturturuz.

En temel üç pisagor bağıntısı şu şekildedir:

1. b² = h² + (n + x)²
2. c² = h² + (m - x)²
3. d² = h² + x²

İlk eşitliği m ile, ikinci eşitliği ise n ile genişletip ardından taraf tarafa toplayalım.

• b²m = h²m + n²m + 2mnx + x²m
• c²n = h²n + m²n − 2mnx + x²n

Toplarsak şöyle bir sonuç elde ederiz;

b²m + c²n = (m + n)(h² + mn + x²) = (m + n)(d² + mn)

Bu işlemden sonra da (m+n) karşıya bölüm olarak atılırsa;

(d² + mn) = (b²m + c²n) / (m + n) olur. Ardından da m.n karşı tarafa eksi olarak atılır ve formül bu şekilde elde edilir:

d² = (c².n + b².m) / (m + n) - m.n